Sistem Bilangan Biner

Bagi yang sering bersentuhan dengan Komputer apalagi seorang Programmer dan Ahli jaringan pasti mengetahui apa itu Bilangan Biner.

Bilangan Biner adalah sebuah bilangan yang berbasis 2, yaitu 0 dan 1.

Gottfried Wilhelm Leibniz

Sistem bilangan biner modern ditemukan oleh Gottfried Wilhelm Leibniz pada abad ke-17.
Sistem bilangan ini merupakan dasar dari semua sistem bilangan berbasis digital.
Sistem ini juga dapat kita sebut dengan istilah bit, atau Binary Digit.
Dalam istilah komputer, 1 Byte = 8 bit.
Bilangan biner digunakan dalam sistem komputer dan merupakan bahasa paling dasar dalam komputer yaitu Bahasa Mesin.

ASCII

Kode-kode rancang bangun komputer, seperti ASCII, American Standard Code for Information Interchange menggunakan sistem peng-kode-an 1 Byte.

notasi yang digunakan dalam sistem digital:
- 4 bits = Nibble
- 8 bits = Byte
- 16 bits = Word
- 32 bits = Double word
- 64 bits = Quad Word (or paragraph)

 Ciri suatu bilangan menggunakan sistem bilangan biner adalah adanya tambahan subskrip bin atau 2 di akhir suatu bilangan (hanya saja ciri ini jarang ditemukan karena bentuk bilangan biner yang mudah diketahui).
Contoh: 1101 1001_bin = 1101 1001₂.

1111 1111 merupakan nilai maksimal bentuk biner yang dapat tersimpan dalam 1 byte.

Bilangan biner juga membangun sebuah IP address
- IPv4 mengunakan 34 bit pengalamatan, yang berarti mempunyai ruang alamat sebesar 2³² = 4.294.967.296
- IPv6 mengunakan 128 bit pengalamatan, yangberarti mempunyai ruang alamat sebesar 2¹²⁸=3,4 x 10³⁸

Berikut beberapa angka desimal yang dijadikan bit:

Desimal	Biner (8 bit )	Desimal	Biner	Desimal	Biner
0	0000 0000	50	0011 0010	100	0110 0100
1	0000 0001	51	0011 0011	101	0110 0101
2	0000 0010	52	0011 0100	102	0110 0110
3	0000 0011	53	0011 0101	103	0110 0111
4	0000 0100	54	0011 0110	104	0110 1000
5	0000 0101	55	0011 0111	105	0110 1001
6	0000 0110	56	0011 1000	106	0110 1010
7	0000 0111	57	0011 1001	107	0110 1011
8	0000 1000	58	0011 1010	108	0110 1100
9	0000 1001	59	0011 1011	109	0110 1101
10	0000 1010	60	0011 1100	110	0110 1110
11	0000 1011	61	0011 1101	111	0110 1111
12	0000 1100	62	0011 1110	112	0111 0000
13	0000 1101	63	0011 1111	113	0111 0001
14	0000 1110	64	0100 0000	114	0111 0010
15	0000 1111	65	0100 0001	115	0111 0011
16	0001 0000	66	0100 0010	116	0111 0100

angka masing-masing digolongkan sebagai bit
- Bit di paling kanan pada bilangan biner, dikenal sebagai bit yang tidak signifikan (Least Significant Bit  = LSB).
- Bit di paling kiri pada bilangan biner, dikenal sebagai bit yang paling signifikan (Most significant bit = MSB)

Penjumlahan Pada Bilangan Biner
Penjumlahan biner terbilang cukup mudah, dikarenakan hanya bebasis 2, yaitu 0 dan 1.
Caranya juga sama dengan penjumlahan desimal.
Contoh:
Pengurangan Pada Bilangan Biner
Pengurangan biner terbilang cukup mudah, dikarenakan hanya bebasis 2, yaitu 0 dan 1.
Caranya juga sama dengan pengurangan desimal.
Apabila yang dikurangi lebih kecil daripada pengurangnya, maka digunakan sistem borrow (pinjaman) dari kolom sebelah kirinya.
Nilai 1 borrow adalah basis dari biner yaitu 2.
Contoh:
Perkalian Pada Bilangan Biner
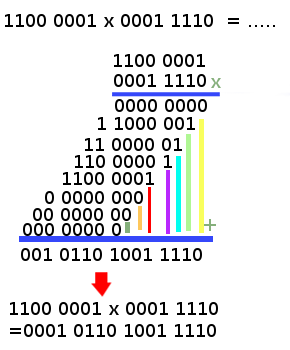
Perkalian Biner mirip dengan perkalian desimal.
Contoh:
Pembagian Pada Bilangan Biner
Cara pembagiannya mirip dengan pembagian desimal.
Contoh:
Konvensi Bilangan Desimal Ke Bilangan Biner
Cara Konvensi Desimal ke Biner adalah dengan melakukan operasi modulus pembagian 2.
Kita akan coba untuk membuat IP 231.7.139.111 menjadi sebuah biner.
Maka Hasilnya: 1110 0111 . 0000 01111 . 1000 1011 . 0110 1111
Konvensi Juga dapat dilakukan dengan Program Excel, seperti LibreOffice yang bernama LibreOffice-Calc dengan Rumus "=DEC2BIN( 'angka' )".

Konvensi Bilangan Biner Ke Bilangan Desimal
Konvensi Bilangan Biner ke Desimal lebih gampang, yang dibutuhkan adalah kemampuan dalam pemangkatan:
Kita akan coba dengan: 1100 0001 . 1000 0011 . 0001 1011 . 1111 1111

Konvensi Juga dapat dilakukan dengan Program Excel, seperti LibreOffice yang bernama LibreOffice-Calc dengan Rumus "=BIN2DEC( 'angka' )".

Berikut hasil-hasil dari pemangkatan angka 2:

Bilangan Pangkat	Hasil Pemangkatan	Bilangan Pangkat	Hasil Pemangkatan	Bilangan Pangkat	Hasil Pemangkatan
20	1	217	131.072	234	17.179.869.184
21	2	218	262.144	235	34.359.738.368
22	4	219	524.288	236	68.719.476.736
23	8	220	1.048.576	237	137.438.953.472
24	16	221	2.097.152	238	274.877.906.944
25	32	222	4.194.304	239	549.755.813.888
26	64	223	8.388.608	240	1,099511628×10¹²
27	128	224	16.777.216	241	2,199023256×10¹²
28	256	225	33.554.432	242	4,398046511×10¹²
29	512	226	67.108.864	243	8,796093022×10¹²
210	1.024	227	134.217.728	244	1,759218604×10¹³
211	2.048	228	268.435.456	245	3,518437209×10¹³
212	4.096	229	536.870.912	246	7,036874418×10¹³
213	8.192	230	1.073.741.824	247	1,407374884×10¹⁴
214	16.384	231	2.147.483.648	248	2,814749767×10¹⁴
215	32.768	232	4.294.967.296	249	5,629499534×10¹⁴
216	65.536	233	8.589.934.592	250	1,125899907×10¹⁵

Dengan Bilangan Biner, kita juga bisa membuatnya bermakna Huruf Alfabet. Untuk hal itu dapat dilihat di tabel berikut:

Huruf Alfabet Besar	Biner	Huruf Alfabet Kecil	Biner
A	0100 0001	a	0110 0001
B	0100 0010	b	0110 0010
C	0100 0011	c	0110 0011
D	0100 0100	d	0110 0100
E	0100 0101	e	0110 0101
F	0100 0110	f	0110 0110
G	0100 0111	g	0110 0111
H	0100 1000	h	0110 1000
I	0100 1001	i	0110 1001
J	0100 1010	j	0110 1010
K	0100 1011	k	0110 1011
L	0100 1100	l	0110 1100
M	0100 1101	m	0110 1101
N	0100 1110	n	0110 1110
O	0100 1111	o	0110 1111
P	0101 0000	p	0111 0000
Q	0101 0001	q	0111 0001
R	0101 0010	r	0111 0010
S	0101 0011	s	0111 0011
T	0101 0100	t	0111 0100
U	0101 0101	u	0111 0101
V	0101 0110	v	0111 0110
W	0101 0111	w	0111 0111
X	0101 1000	x	0111 1000
Y	0101 1001	y	0111 1001
Z	0101 1010	z	0111 1010

Ok, mungkin itu aja.
Semoga bermanfaat :D.